賭王何鴻燊接手葡京賭場時,業務蒸蒸日上,但理性的賭王仍然忐忑,請教「賭神」葉漢:「如果這些賭客總是輸,長此以往,他們不來了怎麼辦?」葉漢笑道:「一次賭徒,一世賭徒,他們擔心的是賭場不在怎麼辦。」

賭徒迷信的是運氣 賭場相信的是數學

葉漢說的只是心理層面,現代賭場程序方面的設計,比葉漢當年要縝密得多,賭場集中了概率、級數、極限方面的數學經驗。一個普通賭徒,只要長久賭下去,最終一定會血本無歸,所謂的各種致勝絕技,除了電影里的周星星,現實里的周星馳都不信。
賭徒永遠不明白,與自己對賭的不是運氣,也不是莊家,他們是在與狄利克雷、伯努利、高斯、納什、凱利這樣的大師對決數學,贏的勝率能有多大?
看得到的是概率 看不見的是陷阱
我們先說一個最簡單的賭博遊戲:賭運氣猜硬幣。
規則是這樣的,擲硬幣,正面贏反面輸,贏了可以拿走一倍的錢,輸了會賠掉本金,你玩不玩?你可能覺得,唉,這遊戲不錯,公平!恰好運氣也不錯,第一把贏了100元!你高興壞了,這時候莊家跟你說,你看你也贏了這麼多,我呢,辛辛苦苦搭個場子,最後什麼都沒撈着,要不這樣,你贏了,就給我留下2%,就算是救濟救濟老哥,給捧捧場!你一聽,2%,才這麼點,拿去吧,不差錢!好了,這事就這麼定下來了。
然而你做夢都想不到的是:就是這小小的2%,最後卻讓你輸得傾家蕩產、家破人亡。
這小小的2個點的贏的概率貌似不起眼,但配上「大數法則」,就成為了賭場賺錢的利器!「大數法則」是數學家伯努利提出來的,說的是假設n(a)是n次獨立重複實驗中發生a的次數,p是每次實驗發生a的概率,當n足夠大的時候,對任意正數ε,有lim{[|(n(a)/n)| p]<ε}=1,公式這麼複雜,99%的賭徒都看不懂,看不懂沒關係,我們只看結果,最終莊家贏到的錢=0.02*a。
莊家賺的錢最終只跟玩家下注大小有關!這也就是我們常說的「流水」,只要玩家不停地玩,莊家就會不停地賺!而不管玩家是輸是贏,莊家始終是贏的!為什麼賭場有「最小投注額」,因為擴大「流水」才能將利潤最大化!
所以別以為自己有多聰明,你要慶幸自己玩得不夠久而已,十賭九輸正源於此。
只要進了賭場 你就是一個窮鬼
我們再進一步,就算雙方的概率均等,你仍然是一個輸家,這裡涉及到「無限財富」和「賭徒輸光定律」,這個定理在現實生活中有許多應用,如「姓氏消亡」「線粒體夏娃假說」,在概率均等的情況下,誰的資本大,誰的贏率高。
你和我對賭,你我各有5塊錢,輸光為止。那麼你贏的概率是50%,輸的概率也是50%。
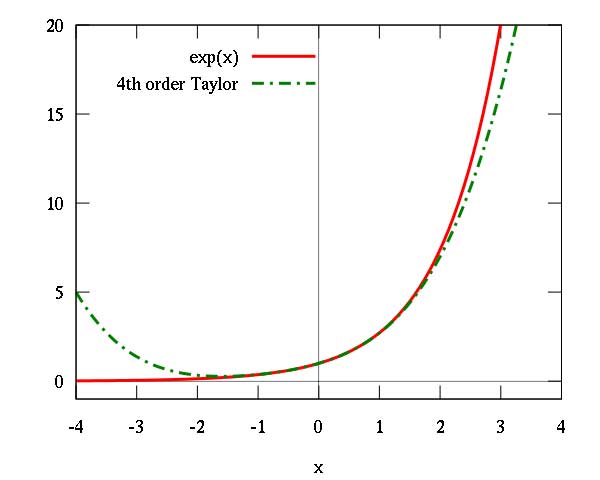
你和我對賭,你有5塊錢,我有10塊錢,輸光為止,那麼你贏的概率就只有33.3%,而輸的概率有66.7%(這裡涉及到高斯的概率論和泰勒的級數論),後面隱藏的就是賭場大BOSS凱利公式,後面小節里將詳加表述。
對於小散戶,賭場一般可以認為財富是無限多的,你贏不垮它,它卻能吃了你。在賭場老闆的眼裡,世界只有兩種人:一種現在是窮鬼,一種未來是窮鬼。
「無限財富定律」也解釋了賭場設置最大投注額原因。不是老闆好心保護賭徒免遭破產,只是老闆為了保護自己設置的安全屏障,想象下萬一哪天比爾蓋茨去賭場找樂子,一次性砸個幾百億進去,那賭場老闆真的要哭了,雖然這種事情不太可能發生,但也不能不防,所以賭場根據自己的財富能力設計最高投注額,也就是為了抵抗「無限財富定理」!
賭場大BOSS凱利公式:先告訴你怎麼下注
凱利公式在高級賭徒的世界里大名鼎鼎,那什麼是凱利公式,我們先看一個例子:
有一個簡單2賠1的賭局,扔硬幣下注,硬幣為正面則得2元,如果為反面則輸掉1元,你的總資產為100元,每一次的押注都可投入任意金額。
你會怎麼賭呢?
如果你是冒險主義者,你可能會想,要玩就玩票大的,一次性把100元全壓上,幸運的話,一次正面就可以獲得200元,又是一段值得炫耀的賭史;可是,如果輸了得把100元資產拱手獻給對方,你就一無所有,好不容易來趟拉斯維加斯,這肯定不是明策。
如果你是保守主義者,你可以會想,謹慎點,百分之一慢慢來。你每次只下注1元,正面贏2元,反面輸1元。玩了20把突然覺得,對方下注10元一次就贏得20元,自己一次才贏2元、10次才能贏得20元,後悔已經錯過幾個億!
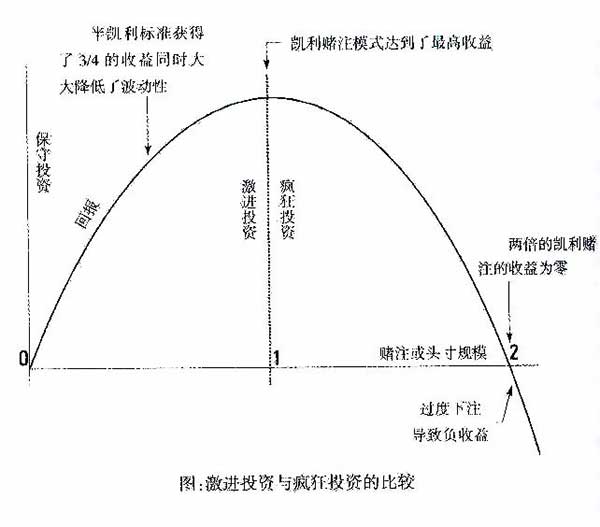
100太多1塊太少,該投入多少比例下注?普通賭徒看似無解,但凱利公式告訴你答案是25%!

讓我們來看看凱利公式的廬山真面目:
f* =(bp-q)/ b
在公式中,各參數意義為:
f* = 應投注的資本比值
p = 獲勝的概率(也就是拋硬幣正面的概率)
q = 失敗的概率,即1 – p(也就是硬幣反面的概率)
b = 賠率,等於期望盈利 ÷可能虧損(也就是盈虧比)
公式上面的分子bp-q代表「贏面」,數學中叫「期望值」。
什麼才是不多不少的合適賭注呢?凱利告訴我們要通過選擇最佳投注比例,才能長期獲得最高盈利。回到前面提到的例子中,硬幣拋出正反面的概率都是50%,所以p、q獲勝失敗的概率都為0.5,而賠率=期望盈利÷可能虧損=2元盈利÷1元虧損,賠率就是2,我們要求的答案是f,也就是(bp – q) ÷ b = (2 * 50% – 50%) ÷ 2 = 25%。
拿出資金的25%來進行下注,才能使賭局收益最大化。
賭場操盤者的每一次下注的時候,都會謹記數學原則,而作為普通賭徒,除了心中默念「菩薩保佑」外,哪裡知道這後面的數理知識。
所以,就算你贏得了財神爺的支持,但你也永遠贏不了「凱利公式」。
除了100%贏 任何時候都不應下注
所有的賭場遊戲,幾乎都是對賭徒不公平的遊戲。
但這種不公平並非是莊家出老千,現代賭場光明正大地依靠數學規則賺取利潤,從某種意義上來講,賭場是最透明公開的場所,如果不是這樣,進出賭場不知有多少狂命之徒,何鴻燊早怕九條命都不夠。
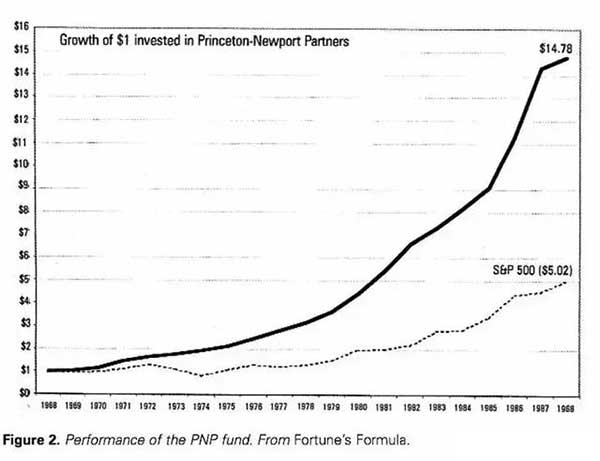
凱利公式不是憑空設想出來的,這個數學模型已經在華爾街得到驗證,除了在賭場被奉為正神,也被稱為「資金管理神器」,是比爾格羅斯等投資大佬的心頭之愛,巴菲特依靠這個公式也賺了不少銀子。回歸到賭場討論這個公式,根據f = (bp-q) / b公式結論,期望值(bp-q)為負時,賭徒不具備任何優勢,也不應下任何賭注。這種賭博遊戲,要下負賭注,也就是說你不如自己開個賭場當莊家。
的確,世界上有為數不多的「賭神」,他們當中有信息論的發明者香農,數學家愛德華·索普,路徑理論的創始人蒙特卡羅等,他們通過一系列複雜的計算和艱深的數學理論,把某些賭戲的贏率扳回到50%以上,例如21點靠強大的心算能力可以把概率拉上去。但就憑你讀書時上課打瞌睡輸了只知道倍投翻本的可憐知識,以及九九乘法表的那點算力,還是先老實讀完以下3條準則。
1、期望值(bp-q)為0時,賭局為公平遊戲,這時不應下任何賭注。
2、期望值(bp-q)為負時,賭徒不具備任何優勢,也不應下任何賭注。
3、期望值(bp-q)為正時,這時按照凱利公式投注賺錢最快,風險最小。
其實最終結論只有一個:除了100%贏,任何時候都不應下全部賭注,即使贏的概率高達99.9%。
結語
贏得勝利的唯一法則:不賭
沒有誰能說服一個墮落的賭徒,因為這是人格的缺陷。
但如果你還是一個具有理性精神的人,別再迷戀所謂的運氣。
賭徒能夠依靠的是祖宗保佑,而賭場後面的大佬是高斯、凱利、伯努利這樣的大神。
你怎麼可能贏得了莊家?
論理性,沒有人能比賭場老闆更理性。
論數學,沒有人能比賭場老闆請的專家更精通數學。
論賭本,沒有人能比賭場老闆的本錢更多。
如果你想真正贏得這場賭局,法則只有一個:不賭。■
來源:量子學派



Be the first to comment